Cassegrain Notes.
Written by Kenneth Novak, BS.
Second Edition
Cassegrain Notes.
Second Edition
First, I'd like to thank the readers of the first edition of Cassegrain Notes that took the time to write and offer suggestions for improvements and also those readers purchasing the first edition. Many improvements have been made in the second edition within the limits imposed by the demand for the booklet, unfortunately, telescope design and construction books have a relatively limited market, otherwise more material could be added. Maybe more can be added in the next printing.
References are given at the end of each Section for additional material. No attempt is made to redo already published material. All parts of a Cassegrain telescope can be made by some skilled amateurs with sufficient equipment and materials. However since most Cass telescopes are built using commercial parts the emphasis is on using them. Commercial parts are carefully designed to fit each other and to minimize assembly, adjustment and use of a Cass telescope. Many special designs are possible requiring special parts but they require special designs to properly support the optics and to use available equipment and materials unless you have the skill, materials and equipment to duplicate special designs the information is of little use. Detailed information on machining Cass parts including the tube and corrector cell are given in "Construction of a Maksutov Telescope" by W. I. Fillmore, Sky Publishing Corp. 1961.
| Page | |
| Cassegrain Optical Designs | 4 |
| Convertible Newtonian and Cassegrain Telescopes | 9 |
| Light Baffles | 14 |
| Telescope tubes | 17 |
| Special Cass Tubing Considerations | 22 |
| Assembling a Cassegrain Telescope | 24 |
| Collimation and adjustments | 27 |
| Typical Figuring of a Cassegrain | 31 |
| An added section, the Cassegrain Forumlas | Cass Formulas |
| Testing Secondaries | Secondary Tests |

The classical Cassegrain telescope design was originated in 1672 by Guillaspe Cassegrain. At the time it could not be used in real telescopes because both the primary mirror and secondary mirror required aspherical surfaces. surfaces. Optical making was limited to spherical surfaces. At about the same time Isaac Newton developed the Newtonian telescope using one aspheric primary mirror and flat secondary mirror. A few of these telescopes were constructed. A few of these telescopes were constructed with spherical surfaces but without the aspheric mirrors the results were not encouraging. It wasn't until 1723 that the first telescope with an aspheric mirror was built - a Newtonian of about F10.5. Today we think of mirrors as pieces of glass with a thin coating of metal. but in the early development of reflectors the mirrors were pieces of metal ground to the proper curve and polished until very shiny. The shiny surface lasted only a few weeks before it had to be re polished and corrected again With all of the problems with the aspheric surfaces and nearly constant re polishing required the effort to develop the reflector telescopes might seem out of place. Refractor lens telescopes that had been in use for decades. However, the refractor lenses in use at the time were uncorrected for color distortion in particular plus many other optical problems. Reflectors were developed to correct most of these optical distortions but especially color. Newtonian and Cassegrain telescopes collect light without passing it thru glass, thus avoiding the color problem. Refractor lenses of very high F-ratio reduce color defects while reflectors can be made fully corrected at any f-ratio including very low f-ratios. Reflector telescopes did not achieve extensive use until methods making aspheric surfaces were developed mainly after Foucault perfected his test and methods of coating glass with metal were developed (silver coatings at first and aluminum coatings for longer life). Early this century reflectors could effectively compete with refractors. Development had greatly improved reflectors. However reflectors could be more easily made in large apertures, very low f-ratios and at low cost. Since a Cassegrain primary mirror is a low f-ratio with a fairly high effective f-ratio gained by the magnification of the secondary, both Newtonian and Cassegrain telescopes, could use much shorter and lighter tubes.
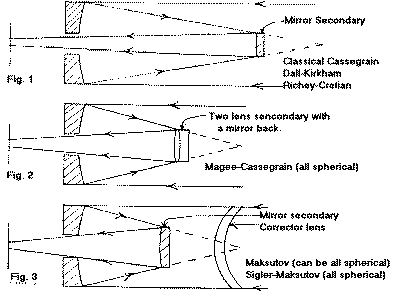
The classical Cassegrain telescope optical system uses a parabolic primary mirror and a hyperbolic secondary. This gives good image correction, except for coma, and a flat field. As the reflector telescope gained popularity early this century technology for making the optics also improved. And variations of he Cassegrain system were developed to improve image corrections and/or make producing the optical surfaces easier. The Gregorian telescope was invented even before the classical Cassegrain. It used a parabolic primary and elliptical secondary. The optical performance is about the same as the Cassegrain is but needs a longer tube. The Gregorian system is a workable optical system but is rarely made as it offers no special advantage over the Cassegrain system and has the disadvantage of a longer tube.
Bernard Schmidt developed the Schmidt principle in the 1930's, taking a spherical primary mirror and usually with a thin aspheric corrector lens but the focal plane is not flat. It has a quite strong curve. The design corrected for coma very nicely. The Schmidt principle has been applied to make Schmidt cameras (both with and without the corrector lens) and to Schmidt-Cassegrain telescopes. The major advantage to the Schmidt principle is to give well corrected images to very low f-ratio cameras and telescopes. In Schmidt cameras the film is usually curved to match the curve of the focal plane. Other designs are made to reduce coma such as the Ritchey-Chretien with hyperbolic curves on both the primary and secondary mirrors. The focal plane can be made fairly flat so when used for photography the film is sometimes only curved slightly to suit. The Maksutov-Cassegrain uses a thick corrector lens over the upper end of the tube but usually all surfaces are spherical. In some cases, one or more of the surfaces are made aspherical in order to get improved correction, especially if the f-ratio is not very high. The coma is not as well corrected as the classical Cassegrain, Ritchey-Chretien, or Schmidt-Cassegrain.
In more recent years these Cassegrain designs have been further modified, often with the help of computers. The Dall-Kirkham-Cassegrain uses an ellipsoidal primary and a spherical secondary mirror to simplify making the optics. Both mirror surfaces are easier to produce by amateurs and optical firms but the aberrations get bad off-axis. The Buchreder-Cassegrain uses all spherical mirrors and a number of spherical refractor relay lenses. The large five all spherical surfaces with the secondary discourage construction. The Magee-Cassegrain has two lens of the Mangin style (rear surface aluminized). Unlike full aperture lenses the refractor secondary lens is easier to make and does not use large pieces of optical glass which is quite expensive. It is limited to fairly small apertures but is usually made with an effective f-ratio of about F8 to give a quite wide field of view for a Cassegrain in a very short tube. The Seigler-Maksutov-Cassegrain has four all spherical surfaces; two in the corrector lens, one in the primary, and one in the secondary mirror. It also is usually made with an effective f-ratio of about F8 to use a very short tube. The Seigler-Maksutov has a special advantage with a well corrected field of 2 degrees and can be made in apertures larger than possible with the Magee-Cassegrain.
Many of these Cassegrain variations are cadioptic, that is, they use a combination of both refractor and reflector optics to collect the light and bring it to the focal plane. This may offer special advantages but tends to discourage construction especially by amateurs. Cassegrain telescopes not ready made are usually classical Cassegrain or Dall-Kirkham either from home made optics or purchased commercial optical sets. The Ritchey=Chretien design could become more popular if optical sets were commercially available. For amateurs with experience making classical Cassegrain optics it might be well to consider the Richey-Chretien since it offers improved corrections over most other optical systems and can be made in large apertures.
 |
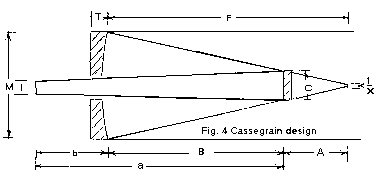 |
| a = (F + b) / (X+1) | where: I = final image size F = focal length of primary b = back focus length X = magnification of Secondary B = separation between mirrors T = thickness of mirror f = f-ratio of primary M = primary mirror dia../ C = secondary clear aperture | |
| Focal length of sec. = B / (X + 1) | ||
| A = a * X = B + b | ||
| Cass effective f-ratio f-ratio = F * X | ||
| I / X = image size at prime focus | ||
| f = F / M |
The formulae for designing Cass telescopes are given here for amateurs making their own optics and amateurs having custom optics made to suit. Stock Cass optics are available at reasonably low cost but most of the above formulae are not needed because there is little choice of all the many variables. You may want to know the magnification of the secondary (X) so you can find the focal length of the primary (F). Use formula
| (1) X = (E - b - B) / B | (2) F = E / X |
Back focus (b); the back focus on a Cass telescope is the distance from the face of the primary mirror to the Cass focus. The back focus must be long enough to bring the final image to a comfortable eyepiece position for the observer , in most Cass telescope the back focus is used up by the mirror thickness (T); Mirror mount (CL distance); height of the focusing mount when fully racked "in" (H); and optical path length of the star diagonal, (OPL). If you have optics made the back focus distance can be selected to match the parts you use. For ready-made optics the mechanical parts might not make up the full back focus distance. The excess can be taken up with focusing mount extensions (placed between the focuser base and the face of the end cap) or by focuser tube extensions (placed between the focuser tube and the eyepiece. To find the proper length of the focusing mount extensions for focuser tube extensions, take the back focal length (b), subtract the distance used by the mirror thickness (T) subtract the CL distance of the mirror mount, subtract focuser height (H) and optical path length used by the star diagonal (OPL). If the remainder is positive, select the next shortest extension within one inch of the remainder. If the remainder is negative you will probably have to use a shorter focusing mount.
STAR DIAGONALS; Star diagonals use up part of the back focus. The light beam from the Cass secondary to the final image is in the same direction as it would be in a normal refractor telescope. Without a star diagonal an observer head must face the same direction as the primary mirror or lens which is up toward the sky. While this can be done; it is very hard on the observors neck especially for objects overhead. To avoid this problem most refractors and Cassegrain type telescope use a star diagonal to allow comfortable observations. Not only does it reflect the light beam near the focus by 90 degrees but since most star diagonals can be rotated 360 degrees in the focusing mount it gives maximum telescope flexibility and observer comfort without rotating the tube. A Cass telescope with its short tube and rotatable star diagonal make it one of the most comfortable and easy to use telescopes available.
In some small Cass telescopes the standard star diagonal is replaced by a diagonal mirror, usually mounted on a single vane holder, positioned in front of the primary mirror. This allows the use of a regular Newtonian type focuser mounted on the side of the tube and avoids the need to cut a hole in the center of the primary mirror times this arrangement must be used because the back focal length is too short for mounting the focuser at the end of the tube. In these cases the tube should be made to rotate as a Newtonian type telescope to allow comfortable eyepiece position.
Star diagonals can be divided into two general types - mirror type and prism type. Since prisms are not color corrected they can cause color problems. The color problems related to prism diagonals vary greatly with the effective f-ratio of the telescope. Prism star diagonals are recommended for use on refractors and Cass telescope of F14 or more. Color distortion is not a problem, the fluorite coating has a very long life, and light loss is less than with a mirror type. Mirror type star diagonals should be used at F12 or less and are recommended at F14 or less to avoid color defects in the images. The mirror coating does not last as long. It is sometimes recoated as needed with the primary and secondary mirrors. Despite these slightly less desirable featured, mirror type star diagonals are very valuable for lower f-ratio Cassegrains and for large star diagonals. Prisms are not generally available to make star diagonals for 2" focusing mounts because of the high cost. Mirror type star diagonals are available in the 2" size when 2" eyepieces are desired to get lower magnifications and wider fields of view.
FOCUSING MOUNTS: The eyepiece focuser also uses up some of the back focal length. a focusing travel of 3" is generally sufficient. If more is needed a focusing tube extension can be added. In most Cass telescopes a standard 1 1/4" eyepiece size is sufficient. A 2" focuser is used only for low f-ratio, wide field, or large aperture Cass telescopes (2" aperture or more).
SEPARATION (B): The distance between the Cass primary and secondary mirrors is called the separation distance. The exact correct separation is determined by the focal length of the secondary. Once the optics are made the separation distance is fixed. Errors in separation can cause deterioration in performance. Some Cass telescopes use a variable separation either by moving the primary or the secondary mirrors to change the back focus. This in turn can focuses the telescope without the use of a focusing mount and allows a telescope to be focused on objects a few feet from the telescope (for bird and animal observations). Some optical performance is sacrificed to get very long focusing range. For an astronomical telescope the objects being observed are effectively all at infinity. The separation should be fixed accurately to match the optical specifications. If you want to use your telescope for observing birds, animals, and other more nearby objects you may need additional 'out' travel for the focuser. It is a very simple matter to add focuser tube extensions as needed between the eyepiece and the focuser. In this way none of the optical performance is sacrificed.
IMAGE SIZE (I): The final Cass image size is formed at the focal plane. Your eyepieces will magnify this image so changing the eyepiece will change the magnification of the telescope. Used here this image size refers to the image size of the full 100 percent illumination. Beyond the circle of 100 percent illumination the image brightness decreases. the 100 percent illumination circle size is selected to be what can best be used by the eyepieces. The size of the 100 percent illumination image circle best to use has been debated by a number of experienced people and varies from 1/4 inch to over a full inch. Selecting an excessively oversized image will increase the size of the secondary. On the other hand a 1/4 inch image size will not bring 100 percent illumination to the full field of view of all eyepieces but usually there is at least 50 precent illumination at the edge. The best practice is to select image size from your own experience to suit your personal preferences and eyepieces. Lacking that here are some guidelines. A 1/2 inch image size is suggested when you plan on using eyepieces mostly of less than 24mm focal length; an image size of 3/4 inch when you plan on using eyepieces often of 24mm to 60mm focal length; and an image size of one inch for prime focus or Cass focus photography for large, extended objects. Refer to "Newtonian Notes" for more discussion on image sizes and to "all about Telescopes" for a chart on the linear field size limits of various eyepieces. The linear field size is what will fit into the eyepiece. The image size at the Cass focus is what you make available for all eyepieces. Only the smaller of the two sizes all match your eye to be used.
CASSEGRAIN SECONDARY SIZE (C): The most commonly used formula for determining the Cass secondary size has been in "Amateur Telescope Making", Book one in the original format. The author, Hohn H. Hindle points out that the formula he gives is approx9imate and yields an undersized answer with respect to the actual required size. The formula given here was derived differently and is exact. Actually the first term
where
| M = primary mirror diameter | X = magnification of the secondary |
| F = focal length of primary | b = back focus |
| I = image size at Cass focus | B = separation |
| Scientific American, August 1972; construction design and optical making of a Magee-Cass |
| Sky and Telescope. Sept. 1975; construction design of Seigler=Maksutov Construction of a Maksutov Telescope by W. I. Fillmore, Sky Publishing Corp., 1961 |
| Maksutov articles from Gleanings for ATM's, Sky Publishing Corp., 1963 |
| Aberrations of a Prism Diagonal, Sky and Telescope, October 1969 |
| Amateur Telescope Making , Book one, Scientific American ; covers Cass optical making |
| Sky and Telescope, November 1968, January 1969; construction of a Buchroeder-Cass |