Glass Selection and Lens Designs

	The Prescription for the Fraunhofer Doublet
	Common Types of Doublets
	Color Correction of the Design

For a mirror maker, choosing glass is a relatively easy matter. Generally, one selects Pyrex from a simple array of standard sizes. But for the lens maker, a glance at the catalog of Schott Glass Technologies (they have a program for selecting their glasses with a lot of nice specs included) or Ohara Corporation (they have a database of their glasses) who are the major suppliers of optical glass world-wide will reveal an avalanche of glass types described in each firm's arcane abbreviations and terminology. Many of these glasses have valuable properties and could be used to make achromatic lenses (some of which are very expensive, but fortunately for the ATM two standard glasses are all one needs to worry about. Schott's BK7 and F2 (the vanilla and chocolate of transmission optics) come in relatively inexpensive, very high quality forms. These two glasses won't make a perfect scope (no two or three glasses will) but will make one that will be quite good, especially for the price.

As for design, I strongly recommend the following standard type, a 6" (150mm) f/15 Fraunhofer aplanat. Many, many other designs exist or could be devised, but this design is easy to build, easy to mount in a lens cell, and performs beautifully. The term "aplanat" means that the lens is corrected for coma, an image aberration which Rutten and & van Venroiij discuss very well in their book. The design is also corrected for chromatic and spherical aberration, meaning that if you follow the design closely (and your glasses are close to the standard values) and polish your glass carefully, there's a good chance that you won't have to do any significant figuring work at the end. Once the glass is polished out and you test it against your autcollimation flat to verify its figure, you may be able to pop it immediately into its lens cell and rush outside to observe the moon, or maybe the double-double in Lyra! No aluminum or any other coating will be necessary. Moreover, so long as the lens is minimally aligned with the tube axis, you'll see no image flare or comatic blur even at high power. Instead, if the seeing is good you'll find a nice round star disk with a faint set of Fresnel rings circumscribing it, just as they should. The ease of testing a lens in autcollimation, combined with the Fraunhofer's aplanatism, means that getting great performance from this type of telescope objective is much easier than from a paraboloidal mirror. Figuring is easy and there's no collimation to do on this design!

Here is the design prescription for our Fraunhofer Telescope (all parameters are given in millimeters):

	Lens Diameter -	156mm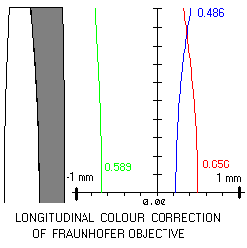
	Clear Aperture -	150mm.
	Glasses -	BK7 and F2 (fine or precision annealed)
	R1 -	1370mm
	Thickness -	14mm - BK7 glass
	R2 -	-800.6mm
	Airgap -	.053mm
	R3 -	-810.6mm
	Thickness -	10.3mm - F2 glass
	R4 -	-3320mm
	Back Focal Length -	2240mm

Don't be frightened by the excessively precise numbers in the dimensions. The precision of the numbers is from the calculation of the values to high precision. One big virtue of an achromat is that its design is actually quite forgiving: the radii can be off by several millimeters before the change will noticeably hurt the lens. What is especially nice is that you can correct many of the errors later by other corrections to the spacing of the lenses when assembling into the finished optic or you can ignore the slightly different center of the achromatic correction. Any decent spherometer will get you that close to this level of accuracy, and the residual aberrations can be corrected in figuring. The thicknesses can vary by even more; the numbers which I've specified above assume that you've started with blanks of 1: 10 aspect ratio (industry standard), in other words 15mm thick pieces of glass. And the airgap isn't critical either as that is usually finalized in the assembly of the lens in it's cell during testing. I assume that you will separate your lenses with three small squares of postage stamp paper thickness placed around their edges at 120 degree intervals. Stamps measure about 0.1mm thick and less when compressed a bit, so if you use them you'll wind up with an airgap between your lenses of about 0.053mm. Adding or subtracting, say, 0.020mm because you used some other spacing material will have a minimal effect. Postage stamps are convenient and traditional.

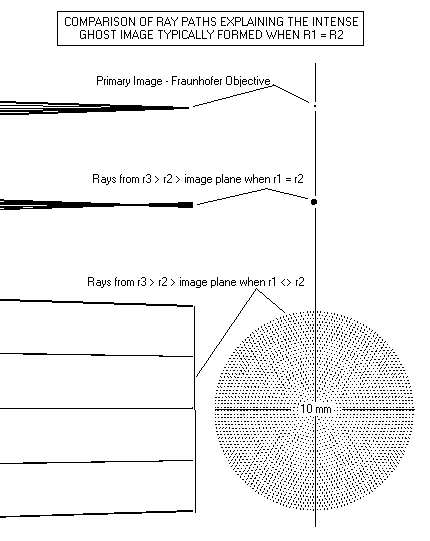The only critical dimension is the difference between R2 and R3, because this affects the residual spherical aberration and the intensity of the ghost reflection caused by light bouncing from R3 to R2 and then back again through the system to focus. Reducing the difference between R2/R3 will intensify the ghost, which will appear as a halo of light around bright objects such as Jupiter and Sirius. Keeping the difference at about 10mm, as above, should defocus the ghost enough to render it always invisible. Putting an anti-reflection coating on these surfaces, although expensive and probably not cost-effective, will totally obliterate this ghost. In my own uncoated 8" f/15 Fraunhofer doublet, I have never seen a ghost image. And from the standpoint of using an achromat, I find it better to keep the lens robust and convenient: uncoated surfaces can quickly be washed in warm water with dish soap and dried off with a clean, soft cotton towel. Using common sense and reasonable care you will not scratch your glass. Whereas, scratched aluminum and AR coatings are the bug bears of other optics. So try to keep R2 and R3 as close to the above specified dimensions as possible.

It is also possible to "scale" the above design to other dimensions by direct linear ratioing. In other words, if you wanted not an f/15, but an f/12, just multiply all the dimensions by 12/15 = 0.8. Or if you want an 8" lens, multiply by 8/6 = 1.333. This will bring you close enough to the numbers you need. Any residual aberrations can be figured away later in autcollimation.

Other designs besides the Fraunhofer may also seem attractive. And in general, with the present availability of optical raytracing software such as ZEMAX or OSLO (a freeware version OSLO-LT is available here), a dedicated amateur can play with may different lens designs and glass types, possibly evolving his or her own favorite. But to my mind, for ease of fabrication, convenience and excellence, the Fraunhofer is the best of the pack.

Several other common lens designs, which an ATM may be attracted to, are:

	the oil-spaced doublet
	the Littrow doublet
	the Clark doublet
	the Fraunhofer doublet

and some designs are noted in the Appendix 1. In the oil-spaced design, the gap between R2 and R3 (these radii now being made equal) is filled not with air, but will some suitable oil, which ideally should have a refractive index between that of crown and flint. In practice, any clean clear oil can be used. Mineral oil, salad oil, even olive oil or cedar oil have all been used. The advantages of oil-spacing is that:

These reasons seem to give one a strong impetus to make an oiled objective. And many successful oiled objectives have been finished. But on the other hand, there can be hidden disadvantages:

The Littrow lens seems to be even easier to build than the oil spaced lens:
R1 = R2 = -R3, and R4 is flat.
In other words, you have an equiconvex crown and a flint with a flat back and an R3 which can serve as a test plate for testing the curves of the crown! What could be better! In practice, only special glass types can be used to make this lens if it is to correct for spherical aberration and/or coma. Moreover, it will show a very strong ghost image, unless R2/R3 are either coated or oiled. And R4 may also produce a ghost image by acting as a kind of autcollimation flat within the telescope tube: stray light from the eyepiece may be re-reflected back to a point and produce a ghost image or general light scatter within the field of view. And finally, flint glass will probably make an unpleasant and weak test plate material, being very prone to scratching. My own experiences with crown glass and even pyrex as test plates suggest that equilibration times will be quite long and mechanical warpage of the lenses lying on top of one another will make it difficult to interpret the optical fringes with confidence.

The Clark lens has the impeccable reputation of the Alvan Clark and Sons firm behind it. It consists of an equiconvex crown (R1 = R2), and a meniscus flint in which R3 is made a few percent shorter in radius than R2. R4 becomes a long radius convex surface. There is much to recommend this lens type and only two drawbacks. It is an airspaced design, similar to the Fraunhofer, but with weaker curves, easier to make well. R1, R2, and R3 are all close in radius to one another, and if you adopt the most obvious version of this lens type spherical aberration can be canceled just as fully as in the Fraunhofer. Moreover, like the Littrow, it's more "customer safe" since if (as often happens with refractor lenses) R1 and R2 become reversed during cleaning, there's no change in performance. Finally, since only three different radii exist in the lens, only three tools need to be made, instead of the Fraunhofer's four.

The drawbacks are these: if you make the most obvious version of the lens, there will be a visible ghost from the R3/R2 reflection (my 6" f/15 Clark-type lens shows this strongly around Jupiter and Sirius). To get rid of this ghost, you'll either need to coat the lens or make the difference between R2/R3 greater. But by doing the latter you'll reintroduce spherical aberration, if you use BK7 and F2, which will then need to be figured away during autcollimation. The lens is not aplanatic, which in practice means simply that collimation matters. You won't get nice round Fresnel rings and the best contrast unless you collimate.

The Fraunhofer lens, by contrast, is coma-corrected and collimation hardly needs to be done: so long as your light path is reasonably square to the tube, you're ready to go! Spherical aberration is fully corrected by the design itself and ghosting is never a problem. The lens curves are stronger, but not unreasonable and not difficult to make well. And the fourth tool is no big deal for an amateur maker. Perhaps the Clarks would always have used this design, if economic incentives of the 19th century had not dissuaded them: the Fraunhofer design required somewhat thicker lens blanks than they liked to use, and the steeper curves and fourth radius required more time to make. Glass and labor costs would have increased the price of their already high-end product.

For all these reasons, I recommend the Fraunhofer design which I have specified above. But the other lens types require fabrication methods virtually identical to what I describe below. If you want to build something else, by all means try it!

Deep red and purple light focus further back and are never in a reasonable focus, but are not very bright and so don't substantially harm the image quality. In fact, though it is perhaps heretical to say, the unfocused purplish color often adds a certain aesthetic charm to double star viewing and to the unappealing brown color or Jupiter's belts. However, it also does somewhat lower contrast and is very bad for photography.

Other color corrections are possible and have been used. In the 19th c. the great makers of lenses preferred to bring red light to a focus closer than blue light, i.e. to "overcorrect" for color. Perhaps this was done because of the natural undercorrection of the eye and the simple eyepieces in use then. Moreover, the flint glasses then used tended to have a residual yellowish hue, and so tended to block blue light. Contemporary flint glass is as clear as water, and all eyepieces now made are achromatic. The lens prescription which I have given above will produce a standard contemporary style achromat.

Still another color correction is the "photographic" correction, often used in the past. This sought to focus the blue and purple rays most sharply to the shortest focus because black and white emulsions were most sensitive to these rays.

Finally, if very long focal ratio achromats are built, it might be worthwhile to achromatize C and the g-line (a more violet line). F/15 or f/12 are the standard focal ratios in which contemporary achromats are built. But f/20 and beyond will produce even better results for color correction, if the long tube lengths can be managed. The color error almost vanishes from visual detection, if the focal ratio is held to 5 times the objective diameter in inches, or 2 time the diameter in centimeters. Unfortunately, this quickly leads to very long tube lengths, but if one can manage a long tube or fold it by means of flats, then achromatizing to the C and g lines may produce even better results.

What type of performance can you expect from a standard visual achromat? The user of a typical Newtonian telescope will likely notice the follow features. First, at low power (5-10X/inch) there is not much noticeable color error. Very bright stars will be fringed with a bluish or purplish haze, but the stars themselves still seem dazzling bright and of an almost identical hue as they show in a reflector. Sirius still looks white, and Betelgeuse looks dark orange. Jupiter, Venus and the Moon look much as the do in reflectors apart from a bluish fringe around them. Star fields typically appear as in a Newtonian, only the stars themselves appear sharper, like intense points instead of slightly soft. Emission nebulae such as M42 or M17 typically show much more contrast than in an equal sized reflector. Indeed, I find that in my 8" refractor a nebula filter usually reduces the contrast rather than improves it. The opposite was always the case for me in reflectors.

At medium powers (20-30X/inch), a tiny blue fuzz and inside of that a red fringe become clearly visible around bright white stars, which begin to take on a tinge of yellow. The planets and moon appear at their best showing intense contrasts and fine, sharp detail, and continue to be colored much as in a reflector, but with a bluish haze around them. It is at these powers that an achromat excels in planetary contrast. On the down side, despite the wealth of detail Jupiter's bands, for example, look purplish instead of brown and the festoons show less contrast than in an apochromat, though they're typically better than in an equal sized reflector. Deep sky objects look wonderful. In good seeing, all six stars of the Trapezium are easily visible in a 6" achromat at about 100X. In my 8", I can clearly see the dark equatorial lanes of NGC 4565 and 891 and M104. And recently, M1 showed a peculiar mottling which I'd never seen before, almost as if the filaments were coming into view. And the propeller feature of M13 is easy to see.

At high powers (40-50X/inch), all bright stars take on a yellowish or orangish hue, surrounded by a fainter blue haze. The objective has become a selective yellow filter. Planets and the moon are generally improved by filters, since the color separation now becomes large. At 400X with a yellow filter in my 8", I was once able to see 8 craterlets inside Plato on the moon. Planetary nebulae show off well, since they radiate brightly at only a few wavelengths. The Eskimo Nebula's central star appears sharp and intense at high power, the nebula itself appearing well defined. And of course, double stars show off very well at high power. My 8" frequently splits Eta Geminorum, Zeta Cancri, Delta Orionis and very close doubles down to 0.5". Occasionally, I can split Omega Leonis, and in good seeing Antares, Nu and Xi Scorpii.

In principle, an achromat should actually be able to split closer doubles than a reflector, because the latter's perfect achromatism brings red light to the same focus as yellow. But the Airy disk's size varies according to the wavelength of light being observed. Since the Airy disk for red light is much larger than for yellow or blue, then an achromat being freed from red light at high power should produce a smaller Airy disk than an equal-sized reflector and thus be able to resolve closer doubles. In practice, however, the difference will be small and probably not observable by an amateur.

For a more detailed description of star-testing an achromat, see H.D. Taylor in the book cited above.